.: บทที่ 1

ระบบเลขฐาน (Binary system)

เลขฐาน หมายถึงกลุ่มข้อมูลที่มีจำนวนหลัก (Digit) ตามชื่อของฐาน
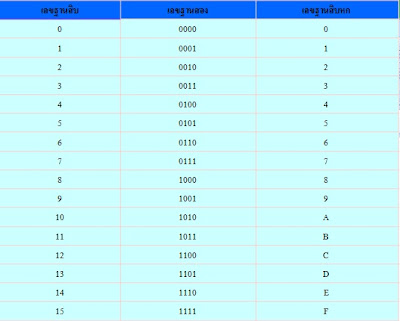
นั้นๆเช่น เลขฐานสอง ฐานแปด และฐานสิบ ประกอบด้วยข้อมูลตัวเลขจำนวนสองหลัก (0-1) แปดหลัก (0-7) และสิบหลัก (0-9) ตามลำดับ ดังรูปในตารางที่ 1
ในระบบคอมพิวเตอร์มีการใช้ระบบเลขฐาน 4 แบบ ประกอบด้วย
     1).เลขฐานสอง (Binary Number)
     2).เลขฐานแปด (Octal Number)
     3).เลขฐานสิบ (Decimal Number)
     4).เลขฐานสิบหก (Hexadecimal Number)

แสดงจำนวนตัวเลข ของเลขฐานต่างๆ

การเขียนตัวเลขในรูปเลขฐานต่างๆ โดยทั่วไปนิยมเขียนตัวเลขระบุฐานกำกับไว้ด้วยเสมอ (ยกเว้นเลขฐานสิบ) เช่น

(1011)₂ หมายถึงเลขฐานสอง

(452)₈ หมายถึงเลขฐานแปด

(1000)₁₀หมายถึงเลขฐานสิบ แต่ทั่วไปไม่เขียนตัวเลขระบุฐานกำกับ

(3C)₁₆หมายถึงเลขฐานสิบหก

เลขฐานสอง(Binary Number)

คือตัวเลขที่มีค่าไม่ซ้ำกันสองหลัก ( 0 และ 1) เป็นเลขฐานเดียวที่เข้ากันได้กับ Hardware ของเครื่องคอมพิวเตอร์ได้โดยตรง เพราะการใช้เลขฐานอื่น จะสร้างความยุ่งยากให้กับเครื่องคอมพิวเตอร์อย่างมาก เช่น เลขฐานสิบมีตัวเลขที่เป็นสถานะที่ต่างกันถึง 10 ตัว ในขณะที่ระบบไฟฟ้ามีเพียง 2 สถานะ ซึ่งในช่วงเวลาหนึ่งๆมีเพียงสถานะเดียวเท่านั้น แต่ละหลักของเลขฐานสอง เรียกว่า Binary Digit (BIT)

เลขฐานแปด(Octal Number)

เลขฐานแปด มีความสัมพันธ์กับเลขฐานสอง คือ เลขฐานสองจำนวน 3 หลัก แทนด้วยเลข
ฐานแปด 1 หลัก ดังนั้นเราจึงสามารถเขียนเลขฐานสอง 6 บิท แทนด้วยเลขฐานแปด 2 บิท การใช้เลขฐานแปดแทนเลขฐานสองทำให้จำนวนบิทสั้นลง

เลขฐานสิบ (Decimal Number)

คือตัวเลขที่มีค่าไม่ซ้ำกันสิบหลัก (0,1,2,…,9) เป็นเลขฐานที่มนุษย์คุ้นเคยและใช้ในชีวิตประจำวันมากที่สุด ตัวเลขที่มีจำนวนมากกว่า 9 ให้ใช้ 10 ซึ่งเป็นการกลับไปใช้เลข 1 และ 0 อีก เพียงแต่ค่าของ 1 เปลี่ยนไปเป็น 10 เท่าของตัวมันเอง เช่น 333 (สามร้อยสามสิบสาม) แม้จะใช้ตัวเลข 3 ทั้งหมด แต่ตำแหน่งของตัวเลขย่อมมีความหมายตามตำแหน่งของแต่ละหลักนั้น กล่าวคือ หลักหน่วยน้อยกว่าหลักสิบ 10 เท่า หลักสิบน้อยกว่าหลักร้อย 10 เท่า ตามลำดับ

เลขฐานสิบหก (Hexadecimal Number)

เลขฐานสิบหก มีความสัมพันธ์กับเลขฐานสอง คือ เลขฐานสองจำนวน 4 หลัก แทนด้วย
เลขฐานสิบหก 1 หลัก ดังนั้นเราจึงสามารถเขียนเลขฐานสอง 8 บิทแทนด้วยเลขฐานสิบหก 2 บิท การใช้เลขฐานสิบหกแทนเลขฐานสองทำให้จำนวนบิทสั้นลง

การเปลี่ยนฐานเลข (Base Number Conversion)

เนื่องจากตัวเลขในแต่ละฐานมี ค่าคงที่เฉพาะ ในแต่ละหลักของตัวเอง เช่นตัวเลข 100 มีค่าเท่ากับหนึ่งร้อยในระบบเลขฐานสิบ แต่ตัวเลข 100 ในระบบ
เลขฐานสอง (อ่านว่า หนึ่ง-ศูนย์-หนึ่ง) ซึ่งมีค่าเท่ากับ 4 เป็นต้น ดังนั้น จึงไม่สามารถนำค่าของเลขฐานใดๆ ไปคำนวณเปรียบเทียบ กับเลขฐานอื่นได้โดยตรง

เมื่อต้องการคำนวณหรือเปรียบเทียบตัวเลข (ประมวลผล) จำเป็นต้องเปลี่ยนฐานเลขเหล่านั้นให้เป็นฐานเดียวกันก่อน การเปลี่ยนฐานเลขสามารถกระทำได้
หลายวิธี ในหน่วยเรียนนี้จะใช้วิธีที่สะดวกที่สุดวิธีหนึ่ง ดังนี้

ตาราง แสดงค่าคงที่เฉพาะในแต่ละหลักของเลขฐานสอง

การเปลี่ยนเลขฐานสอง เป็นเลขฐานสิบ

ให้นำค่าคงที่เฉพาะที่ตรงกับเลข 1 ของฐานสองมารวมกัน เช่นจำนวน (11010)2ประกอบด้วยเลข “1” จำนวน 3 ตัว
เมื่อนำค่าคงที่เฉพาะที่ตรงกับเลข 1 มารวมกัน ทำให้ได้จำนวนในฐานสิบเป็น 16+8+2 = 26 ดังนี้

การเปลี่ยนเลขฐานสิบ เป็นเลขฐานสอง

ให้พิจารณานำค่าคงที่เฉพาะหลักใดๆมารวมกัน เพื่อให้ได้ค่าเท่ากับเลขฐานสิบที่กำหนด จากนั้นเติมเลข “1“ ณ ตำแหน่งที่นำตัวเลขมารวมนั้น เช่น (26)10จะต้องใช้ค่าคงที่เฉพาะรวมกัน 3 หลัก (16+8+2) ดังนั้นจึงเติม “1” ณ ตำแหน่ง
16,8 และ 2 ตามลำดับ ส่วนตำแหน่งที่เหลือให้เติม “0”

นอกจากนี้ยังสามารถเปลี่ยนค่าจากเลขฐานสิบให้เป็นฐานสอง โดยการหารเลขฐานสิบด้วยสองไปเรื่อยๆจะได้เศษจากการหาร คือ เลขฐานสอง ที่ต้องการ ตำแหน่งของเศษที่เกิดจากการหารก็คือกำลังของเลขฐานสอง นั่นคือเศษที่ได้จากการหารครั้งแรกจะคูณด้วย 20 เศษที่ได้จากการหารด้วย 2 ครั้งที่ 2 จะคูณด้วย 2 1เป็นต้น
ตัวอย่างเช่น

ตรรกะกับระบบคอมพิวเตอร์การเปลี่ยนระหว่างเลขฐานอื่น (ระหว่างฐานสอง ฐานแปด ฐานสิบ และฐานสิบหก)

ในที่นี้อธิบายถึงการเปลี่ยนฐานเลข ระหว่างเลขฐานสองฐานแปดฐานสิบและฐานสิบหกซึ่งใช้ในระบบคอมพิวเตอร์ทั่วไป โดยมีหลักการเบื้องต้น 3 ประการ ดังนี้

การเปลี่ยนระหว่างเลขฐานอื่น (ระหว่างฐานสอง ฐานแปด ฐานสิบ และฐานสิบหก)

ในที่นี้จะได้อธิบายถึงการเปลี่ยนฐานเลข ระหว่างเลขฐานสอง ฐานแปด ฐานสิบ และฐานสิบหก ซึ่งใช้ในระบบคอมพิวเตอร์ทั่วไป โดยมีหลักการเบื้องต้น 3 ประการ ดังนี้
(a) เปลี่ยนเลขฐานจากโจทย์ ไปสู่เลขฐานสองก่อน (ใช้เลขฐานสองเป็นตัวเชื่อมไปสู่เลข ฐานอื่น)
(b) เลขฐานแปด 1 หลัก ประกอบด้วยเลขฐานสอง 3 หลัก คือ (111) 2